3. Canopy interception#
Canopy interception is the rainfall that is intercepted by the canopy of a tree and successively evaporates from the leaves. Precipitation that is not intercepted will fall as throughfall or stemflow on the forest floor. Canopy interception can significantly affect infiltration, surface runoff, and evapotranspiration, and reduces the erosive energy of droplets.
The FeST model implements a model to simulate canopy interception that is derived from the SWAT model (Gassman et al., 2007).
The amount of water that can be trapped in the canopy in a given time step, \(C_{t}\), is given by:
where \(C_{\max}\) is the maximum amount of water that can be trapped in the canopy when the canopy is fully developed, \(LAI\) is the current leaf area index of a given day, and \({LAI}_{\max}\), is the maximum leaf area index for the plant.
The actual amount of water stored in the canopy, \(C\), is updated at each computational step, \(\mathrm{\Delta}t\), with the mass conservation equation:
where \(C_{i}\) is the initial amount of water stored in the canopy, \(R\ \) is the rainfall rate, and \(PE\) is the potential evapotranspiration rate.
When canopy storage is filled to the maximum value, \(C_{t}\), the excess rainfall amount is allowed to reach the ground as throughfall, \(T\).
Canopy affects only fraction of ground surface covered by vegetation, so the effective rainfall that reach the ground, \(R_{eff}\), is computed as:
where \(f_{v}\) is the fraction of cell covered by vegetation.
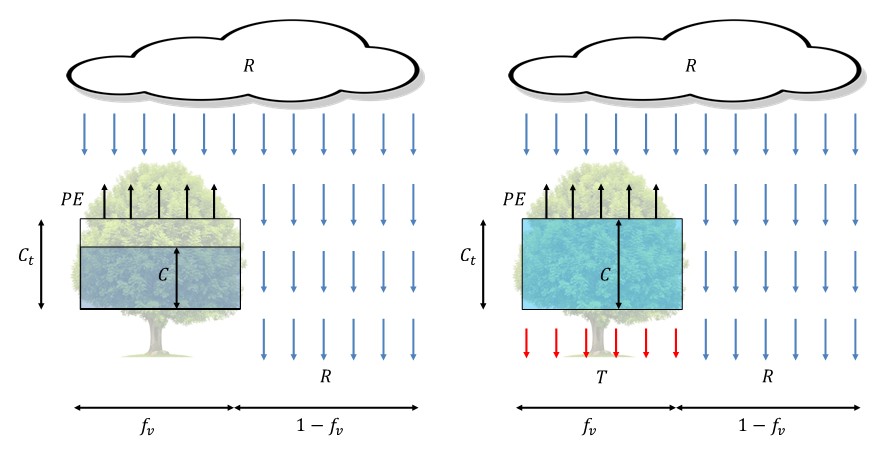
Fig. 3.1 Rainfall is stored in the canopy until the maximum value at a given time, \(C_{t}\), is reached (left). When \(C_{t}\) is reached, the excess rain reaches the ground as throughfall, \(T\) (right).#