4. Snow accumulation and melting

The snow module of FeST includes snow melt and snow accumulation simulation. The partitioning of total precipitation, \(P\), in liquid, \(P_{l}\), and solid,\(P_{s}\), phase is a function of air temperature, \(T_{a}\) (Tarboton et al., 1994):

(4.1)\[P_{l} = \alpha_{P}P\]

(4.2)\[P_{s} = (1 - \alpha_{P})P\]

where \(\alpha_{P}\) is computed by:

(4.3)\[\begin{split}\alpha_{p} = \left\{ \begin{matrix} 0\quad\quad\quad\quad\mspace{6mu} if\quad T_{a} \leq T_{low} \\ 1\quad\quad\quad\quad\mspace{6mu} if\quad T_{a} \geq T_{up} \\ \frac{T_{a} - T_{low}}{T_{up} - T_{low}}\quad\quad if\quad T_{low} < T_{a} < T_{up} \\ \end{matrix} \right.\ \end{split}\]

where \(T_{low}\) and \(T_{up}\) are air temperatures below/above which all precipitation falls as snow/rain, respectively.

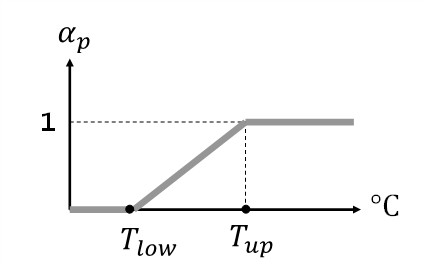
Fig. 4.1 Coefficient of precipitation partitioning, \(\alpha_{p},\ \)in liquid and solid phase

The snow melt simulation is based on the degree day concept (Martinec et al., 1960). The melt rate in m/s, \(M_{s}\), is proportional to the difference between air temperature and a predefined threshold temperature, \(T_{b}\):

(4.4)\[\begin{split}M_{s} = \left\{ \begin{aligned} & C_{m}(T_{a} - T_{b})\quad\mspace{6mu} if\quad T_{a} > T_{b} \\ & 0\quad\quad\quad\quad\mspace{6mu} if\quad T_{a} \leq T_{b} \\ \end{aligned} \right.\ \end{split}\]

where \(C_{m}\) (m °C⁻¹ s⁻¹) is an empirical coefficient depending on meteorological conditions and geographic location.

The mass conservation equation, integrated over duration \(\mathrm{\Delta}t\) , defines the actual snow water equivalent, \(SWE\), stored in each cell:

(4.5)\[SWE = \ \left( P_{s} - M_{s} \right)\ \mathrm{\Delta}t\]

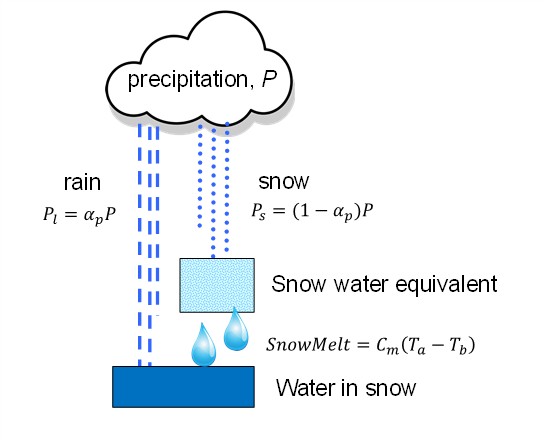
Fig. 4.2 Snow accumulation and melting contribute to the updating of snow water equivalent (SWE) and water stored within snowpack.

The terrain covered by snow is supposed to be frozen and hence the melted water is prevented from infiltrating into the soil. Conversely, the liquid fraction of snow water equivalent, \(R_{s}\), sum of melted water and liquid precipitation, forms the second state variable computed by the snow module:

(4.6)\[R_{s} = \left( P_{l} + M_{s} \right)\ \mathrm{\Delta}t\]

\(R_{s}\) is supposed to flow cell by cell through the snow pack with the Darcy equation, following the flow direction derived from digital elevation model, with a snow conductivity, \(k_{snow}\), of 1.67 10⁻³ m/s (Salandin et al., 2004).

(4.7)\[Q_{snow} = k_{snow}\ \ R_{s}\ \mathrm{\Delta}x\ i\]

where \(Q_{snow}\) is the flux of \(R_{s}\) flowing from cell to cell, \(\mathrm{\Delta}x\) is the cell size, and \(i\) is the local topographic slope.

When \(R_{s}\) reaches a cell not covered by snow, or snow melts totally in the time step, it is treated as an input term in the soil balance of that cell.

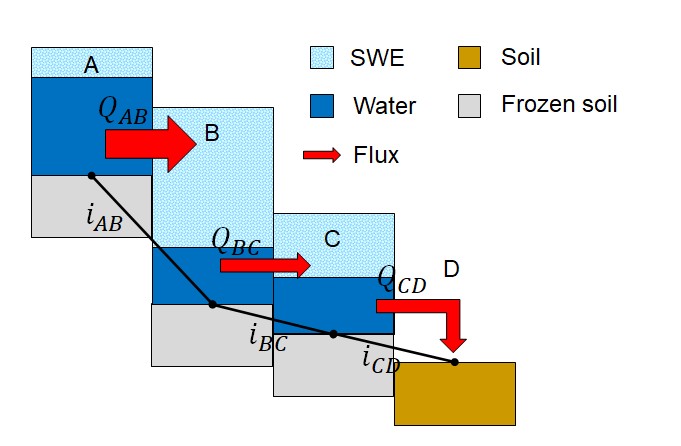
Fig. 4.3 Cells are connected by a lateral flux that transfers water accumulated within snowpack following the flow direction derived from digital elevation model. Flux magnitude is computed with Darcy equation and depends from actual water amount and local terrain slope. When lateral fluxes meets a cell not covered with snow (D), it is treated as a source term in the soil water balance.